三阶贝塞尔曲线
关于贝塞尔曲线,网上很多博客都已经给出了解释,这里通俗的讲一下。
下面的这个图,相信你也看到过很多。然而,我这里也是需要贴一下这个图的。
参数讲解
P0是曲线的开始点P3是曲线的结束点P1和P2是控制曲线走势的控制点,所以这两个点事实上是辅助作用,并不会在画布中被绘制出来
t参数重点讲解
t 是辅助参数,可以看到它的值范围是 [0,1]。这个t值作用于图中的所有直线(P0P1、P1P2、P2P3、两条绿线、蓝线)。
注意:图中真实绘制出来的,就只有红线,其他的都只是辅助的,并不会被真实绘制出来。
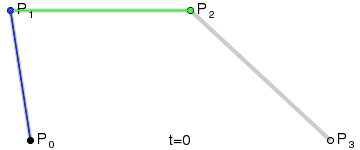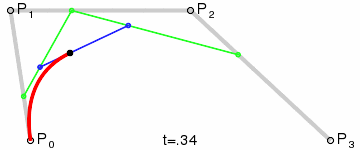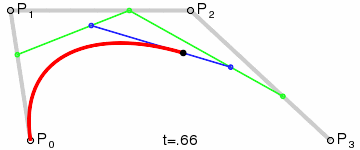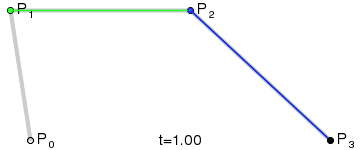
在上图中,你可以看成这个三次贝塞尔曲线由两个二次贝塞尔曲线组成。
- P0P1P2组成的二次贝塞尔曲线
- P1P2P3组成的二次贝塞尔曲线。
所以要把上图的三次贝塞尔曲线拆分成两个二次贝塞尔曲线讲解
例如:
对于第一个二次贝塞尔曲线P0P1P2,
当t=0.5的时候(其实就是[0,1]的中间值,这个比较好理解),情况应该是这样的:
1.找到P0P1线(方向P0->P1,这是有方向的线段)的50% (因为t=0.5,即0.5*100%) 的位置,标上一个绿色的点
2.同1步骤,在P1P2线上的50%位置上标上一个绿色的点
3.把步骤1和2的绿色点连成一条线
4.然后在这条绿色的50%位置处标上一个红点,这个红点就是实际绘制的曲线中的一个点。(当t值不断变化,就会出现不同位置的红点,组成一条曲线)
同理,
第二个二次贝塞尔曲线的理解跟第一个二次贝塞尔曲线一样!
设计图还原
看到这里你也许会问:设计师给了设计稿给我,怎么才能把设计稿里面的曲线还原出来?!
在PS里面,画弧线使用钢笔工具的,所以跟我们的原理是一样的,只要设计师给出开始点,结束点,控制点就OK啦。
canvas中绘制三阶贝塞尔曲线
// 可以用如下方式绘制一条三阶贝塞尔曲线
ctx.moveTo(startX, startY)
ctx.bezierCurveTo(cp1x, cp1y, cp2x, cp2y, endX, endY)
ctx.stroke()
// 也可以利用Path2D把这条贝塞尔曲线缓存,下次直接传入绘制
const path = new Path2D()
path.moveTo(startX, startY)
path.bezierCurveTo(cp1x, cp1y, cp2x, cp2y, endX, endY)
ctx.stroke(path)如何判断一个坐标点是否在三阶贝塞尔曲线附近
有两种做法:
- 一种是使用
CanvasRenderingContext2D内置的方法 isPointInPath:ctx.isPointInPath(path, x, y)进行判断。 - 一种是将已有的三阶贝塞尔公式反推出 t。
interface BezierParams {
startX: number
startY: number
cp1x: number
cp1y: number
cp2x: number
cp2y: number
endX: number
endY: number
}
/**
* @desc 获取三阶贝塞尔曲线的线上坐标
* B(t) = P0 * (1-t)^3 + 3 * P1 * t * (1-t)^2 + 3 * P2 * t^2 * (1-t) + P3 * t^3, t ∈ [0,1]
* @param {number} t 当前百分比
* @param {Array} p1 起点坐标
* @param {Array} p2 终点坐标
* @param {Array} cp1 控制点1
* @param {Array} cp2 控制点2
*/
export const getThreeBezierPoint = (
t: number, p1: [number, number], cp1: [number, number],
cp2: [number, number], p2: [number, number]
): [number, number] => {
const [x1, y1] = p1
const [x2, y2] = p2
const [cx1, cy1] = cp1
const [cx2, cy2] = cp2
const x =
x1 * (1 - t) * (1 - t) * (1 - t) +
3 * cx1 * t * (1 - t) * (1 - t) +
3 * cx2 * t * t * (1 - t) +
x2 * t * t * t
const y =
y1 * (1 - t) * (1 - t) * (1 - t) +
3 * cy1 * t * (1 - t) * (1 - t) +
3 * cy2 * t * t * (1 - t) +
y2 * t * t * t
return [x, y]
}
/**
* @desc 已知四个控制点,及曲线中的某一个点的 x/y,反推求 t
* @param {number} x1 起点 x/y
* @param {number} x2 控制点1 x/y
* @param {number} x3 控制点2 x/y
* @param {number} x4 终点 x/y
* @param {number} X 曲线中的某个点 x/y
* @returns {number[]} t[]
*/
export const getBezierT = (x1: number, x2: number, x3: number, x4: number, X: number) => {
const a = -x1 + 3 * x2 - 3 * x3 + x4
const b = 3 * x1 - 6 * x2 + 3 * x3
const c = -3 * x1 + 3 * x2
const d = x1 - X
// 盛金公式, 预先需满足, a !== 0
// 判别式
const A = Math.pow(b, 2) - 3 * a * c
const B = b * c - 9 * a * d
const C = Math.pow(c, 2) - 3 * b * d
const delta = Math.pow(B, 2) - 4 * A * C
let t1 = -100, t2 = -100, t3 = -100
// 3个相同实数根
if (A === B && A === 0) {
t1 = -b / (3 * a)
t2 = -c / b
t3 = -3 * d / c
return [t1, t2, t3]
}
// 1个实数根和1对共轭复数根
if (delta > 0) {
const v = Math.pow(B, 2) - 4 * A * C
const xsv = v < 0 ? -1 : 1
const m1 = A * b + 3 * a * (-B + (v * xsv) ** (1 / 2) * xsv) / 2
const m2 = A * b + 3 * a * (-B - (v * xsv) ** (1 / 2) * xsv) / 2
const xs1 = m1 < 0 ? -1 : 1
const xs2 = m2 < 0 ? -1 : 1
t1 = (-b - (m1 * xs1) ** (1 / 3) * xs1 - (m2 * xs2) ** (1 / 3) * xs2) / (3 * a)
// 涉及虚数,可不考虑。i ** 2 = -1
}
// 3个实数根
if (delta === 0) {
const K = B / A
t1 = -b / a + K
t2 = t3 = -K / 2
}
// 3个不相等实数根
if (delta < 0) {
const xsA = A < 0 ? -1 : 1
const T = (2 * A * b - 3 * a * B) / (2 * (A * xsA) ** (3 / 2) * xsA)
const theta = Math.acos(T)
if (A > 0 && T < 1 && T > -1) {
t1 = (-b - 2 * A ** (1 / 2) * Math.cos(theta / 3)) / (3 * a)
t2 = (-b + A ** (1 / 2) * (Math.cos(theta / 3) + 3 ** (1 / 2) * Math.sin(theta / 3))) / (3 * a)
t3 = (-b + A ** (1 / 2) * (Math.cos(theta / 3) - 3 ** (1 / 2) * Math.sin(theta / 3))) / (3 * a)
}
}
return [t1, t2, t3]
}
/**
* @desc 传入坐标点判断是否落在三阶贝塞尔曲线上
* @param offsetX 要检测的x轴坐标
* @param offsetY 要检测的y轴坐标
* @param bezierParams 三阶贝塞尔曲线参数
* @returns {boolean}
*/
export const isAboveLine = (offsetX: number, offsetY: number, bezierParams: BezierParams) => {
const {
startX, startY,
cp1x, cp1y,
cp2x, cp2y,
endX, endY,
} = bezierParams
// 用 x 求出对应的 t,用 t 求相应位置的 y,再比较得出的 y 与 offsetY 之间的差值
const tsx = getBezierT(startX, cp1x, cp2x, endX, offsetX)
for (let x = 0; x < 3; x++) {
if (tsx[x] <= 1 && tsx[x] >= 0) {
const ny = getThreeBezierPoint(tsx[x], [startX, startY], [cp1x, cp1y], [cp2x, cp2y], [endX, endY])
if (Math.abs(ny[1] - offsetY) < 8) {
return true
}
}
}
// 如果上述没有结果,则用 y 求出对应的 t,再用 t 求出对应的 x,与 offsetX 进行匹配
const tsy = getBezierT(startY, cp1y, cp2y, endY, offsetY)
for (let y = 0; y < 3; y++) {
if (tsy[y] <= 1 && tsy[y] >= 0) {
const nx = getThreeBezierPoint(tsy[y], [startX, startY], [cp1x, cp1y], [cp2x, cp2y], [endX, endY])
if (Math.abs(nx[0] - offsetX) < 8) {
return true
}
}
}
return false
}这里讲一下为什么推荐第二种方法。
一般在canvas绘制时,由于处理1像素问题(dpr问题),会对canvas进行 scale(dpr, dpr) 处理,并且很多场景下画布都是可拖拽/放大缩小的,这时候即改变了scale又改变了translate。并且如果你对你的canvas进行了优化,很有可能有多个canvas元素。这时候用 isPointInPath 来进行判断就会有诸多不可预见的问题,在进行isPointInPath判断前需要把canvas的坐标系、缩放比例等进行调整才能让程序作出正确的判断。这时候使用第二种 isAboveLine 方法的优势就出来了,不需要考虑坐标系、缩放比例问题,只需要传入坐标系即可做出正确的判断,并且可以自由的定制事件触发的缓冲区。